Quadratic Equation Solver

A= B= C= Significant figures for decimal approximation (up to 20) X = Or X = The exact solution (You may need to simplify this): X = Additional Info: Deriving the Quadratic Formula To Derive the quadratic formula we must complete the square. ax2 + bx + c = 0 First we divide by a: x2 +(b/a)x + c/a = 0 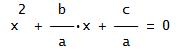    Then we subtract C/a from both sides: x2 +(b/a)x = -c/a 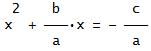    Now for completing the square. Take 1/2 of the (b/a) and square it: That gives (b/(2a))2 = b2/(4a2). Add that to both sides of the equation: x2 + (b/a)x + (b/(2a))2 = b2/(4a2) - c/a 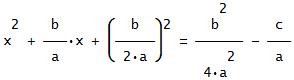    You might notice that on the left side of the equation I left b2/(4a2) in the form of (b/(2a))2 because that makes it easier to factor when you're completing the square, I think. You don't have to do that; it's up to you. Now we factor the left side of the equation: (x + b/(2a))2 = b2/(4a2) - c/a 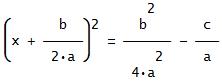    To make things a bit prettier, we get a common denominator (damn-nominator (sic)) on the right side: (x + b/(2a))2 = b2/(4a2) - 4ac/(4a2) 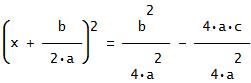    (x + b/(2a))2 = [b2 - 4ac]/(4a2) 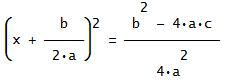    Now we take the square root of both sides, and don't forget when you do that you get ±. Why? Because if you have x2 = 4, the answer is not x = 2, but x = ±2. Now we continue: x + b/(2a) = ±√[b2 - 4ac]/(2a) 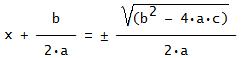    Note that the term 2a is not in the radical. Now all that's left to do is subtract b/(2a) from both sides and we've got the final answer x = (-b ±√[b2 - 4ac])/(2a) 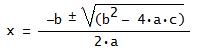    Done! Hint for Using the Quadratic Formula! To use the quadratic formula, especially when negative numbers are concerned, I always use parentheses to substitute in the numbers. For example to solve the quadratic equation -2x2 + 16x - 19 = 0 what I do is this: x = (-b ±√(b2 - 4ac)/(2a) x = (-( )±√(( )2 - 4( )( ))/(2( )) x = (-(16)±√((16)2 - 4(-2)(-19))/(2(-2)) You'll notice that this helps to elliminate any errors from putting in negative numbers! The final simplified answer is x = 4 ±√(26)/2 Hope this helps you! Remember, math is 90% practice, 10% theory. Practice your homework problems! A YouTube video of a Quadratic Formula Mnemonic Song (to Pop Goes the Weasel): Homepage: www.tutor-homework.com More math tools, links, & tutorials:Math Tools & Links